Cosmology, Special Relativity and the Milne Universe
When people study cosmology, the universe is taken to be homogenous and isotropic. There is no evidence that we occupy a special place in the universe, and so cosmologists are very wary of anything that suggests that we might do so. For this reason they like to choose a coordinate system to describe the universe which reflects this symmetry, and in particular a time coordinate which treats all places equally. Unfortunately this leads to a coordinate system which disagrees with the ideas of special relativity, and this can lead to some confusion. I would like to suggest that for some purposes it might be better to choose a more 'special relativistic' coordinate system.
A simple model of the universe
In order to model the expansion of the universe we give each object a proper time τ and a radial coordinate R (Spherical symmetry means that we can ignore the other 2 coordinates). It is simpler if we separate R into a scale factor a(τ) and a scale free distance ψ so that R=a(τ)ψ. Einstein's equations of general relativity then allow us to calculate the form of a(τ). For our simple model, we'll ignore the effects of gravity. In this case we get
a(τ)=kτ
Suppose we (at ψ=0) want to use a coordinate system with a constant speed of light. Then we imagine that we send out a radar beam at time τ0 to the point (τ,ψ) and receive a reflected signal at time τ1. Then we would give this point a time t=(τ1+τ0)/2 and a distance x=(τ1-τ0)/2 (taking the speed of light to be 1). So how does the coordinate (t,x) relate to the coordinate (τ,ψ) ? Well, we have:
| The details of cosmological calculations can be found in chapter 5 of Wald's book General Relativity. More details of this cosmological model can be found on Matt Mcirvin's page on Milne cosmology and in Ned Wright's cosmology tutorial, |
| ψ = | ∫ |
|
| = | ∫ |
|
|
| log |
| = |
| log |
|
| ψ= |
| log | ( |
| ) |
Finally we obtain x=τ sinh kψ and t=τ cosh kψ
Note that in the cosmological coordinates an object had a constant velocity kψ. In the new coordinates this velocity is transformed to tanh kψ, which is always less than 1 (the speed of light). You might like to check that this velocity leads to the appropriate time dilation factor to get back to τ
The above model of the universe was first proposed by E.A. Milne in the 1930's. He called it the kinematic cosmology, but I shall refer to it as the Milne cosmology or Milne universe.
A critical density model
The above considerations show how cosmological coordinates can be transformed to SR coordinates when we know that special relativity holds true. However we can follow the same procedure for other models of the universe. Recent observations suggest that our universe actually has the critical density, although the majority of this is made up of dark energy - i.e. a non-zero cosmological constant. For simplicity we'll look at the case of a critical density, matter dominated, model with zero cosmological constant. In this case we have
a (τ)=(9C/4) 1/3τ 2/3
A similar argument to that above then gives:
t = τ+3τ 1/3ψ 2 and x = 3τ 2/3ψ+ψ 3
So you see that the possibility of choosing 'Special Relativity' type coordinates isn't only possible in a universe with no spacetime curvature.
Some comments
Sometimes people claim that trying to deal with cosmology in the above manner is a return to pre-Copernican ideas, where there is a definite centre to the universe. This seems strange to me. Galileo showed that we do not need to assume a preferred frame of reference for mechanics. Then along came Einstein with special relativity. Was this the re-introduction of a preferred frame of reference? I don't think so! Note also that Milne was an early proponent of the Cosmological Principle, the idea that the universe is the same everywhere.
Another thing to note is that the critical density universe is said to be flat, which means that a circle will have circumference of 2π times the radius. However, the space of the Milne universe is the familiar one of special relativity, which is also said to be flat. There is something strange here, because both of them can't be flat. The thing is that whether you consider a space to be flat depends on the corresponding time coordinate - the circumference of a circle in an expanding universe depends on when you measure it. The critical density space is flat if you use the cosmological time coordinate, whereas the Milne space is flat if you use the special relativistic time coordinate. Using the cosmological time coordinate gives the Milne space a hyperbolic geometry.
Milne's Ideas
| You can see from the Ned Wright's diagrams that there isn't so much difference between flat spacetime and curved spacetime. The paper Expanding Confusion: common misconceptions of cosmological horizons shows how recent observations disagree with the Milne cosmology (there called the SR model). Note that the authors report that they attempted to reject the special relativistic way of looking at things using time dilation. However, they found that it gave the same result as the usual way, which is what you would expect if it's only a coordinate change. |
I should note here that Milne wasn't just presenting his cosmology as an academic exercise - he was presenting it as a model of the actual universe. He didn't like the idea of curved space, and so did without it. Now you may think that curved spacetime is vital to explain anything in cosmology, but in fact its effects are fairly small - measurable today perhaps, but not in the 1930's.
It appears to me that Milne believed that gravitational forces could cancel each other out. This seems odd to those of us used to General relativity, where Einstein introduced the cosmological constant to balance gravity and obtain a static universe. However, Newton also claimed that the universe was static because gravity cancelled out, and I feel it was just as doubtful for Newton as it was for Milne.
Another reason is that Milne didn't like the idea of particle horizons, which are not present in his cosmology. The existence of particle horizons means that more and more of the universe comes into our past light cone as time goes on. Milne rejected this because he considered it to be continuous creation of matter.
So what's the point of this?
| The paper Solutions to the tethered galaxy problem in an expanding universe and the observation of receding blueshifted objects looks at the case of a receding galaxy emitting a jet towards us with the opposite velocity. They find that the jet would in fact be blueshifted. However, in SR coordinates the recession velocity would be less, so the jet would have a net velocity towards us, explaining the blueshift. |
The question is sometimes asked: - How come the Cosmic background radiation we are seeing now took so long to get here. After all, it can't have been that far away from us when it was emitted. Using special relativistic coordinates gives the answer - time dilation delayed the time of emission to about half the age of the universe, and by then the emitting matter (moving away from us at nearly the speed of light), was a long way away. The radiation has taken the other half of the universe's age to reach us. This may seem a weird way of looking at the situation but it does put things into reasonably familiar terms.
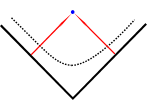
As I've mentioned particle horizons don't occur in Milne's cosmology, but interestingly the use of SR coordinates can give some insight into this phenomenon in other models. In the diagram the big bang can be thought of as being 'spread out' along the sides, and so as time goes on, more of it comes into view.
Well I hope I've shown you that the usual way of looking at the universe isn't the only one, and one can use SR coordinates without disagreeing with general relativity. Next time you hear of something strange going on in cosmology remember to think 'Is this just because of the choice of coordinate system?'.
