Peter Lynds and Zeno's Paradox

References
Time and Classical and Quantum Mechanics : Indeterminacy vs. Discontinuity Peter Lynds Foundations of Physics Letters, 16(4), 2003.
Peter Lynds' homepage
Formal Topology
A general article on Zeno's paradox and its relationship to physics can be found at Zeno's Paradox of the Tortoise and Achilles (PRIME)
An encyclopedia article on Zeno's paradoxes
Another website looking at Peter Lynds' ideas is: The Quantum Machine
When I started reading the papers of Peter Lynds my first thought was 'Topology'. The basic idea of topology is that although most mathematical structures are defined in terms of sets, it isn't sensible to think of the elements just as individual points. Rather, what is important is the closeness relationship between points. This is not defined by the notion of distance between points; rather a topology on a set defines all of the subsets which are neighbourhoods of a point.

In fact Lynds' ideas seem closer to those of Formal Topology which starts from the notion of a set of neighbourhoods without the underlying set. This is the notion that Lynds has developed in his ideas about time - that what is important is the idea of an interval rather than what happens at individual points of time.

Face of clock in hourglass
Artist: George Emmons

A paradox which is similar to Zeno's is that of Thompson's lamp. This is switched on for one second, then off for half a second, then on for quarter of a second then off for an eighth of a second and so on. The question is: is it on or off at the end of two seconds. .Paradoxes like this aren't really there to be solved, but to help you to think about time. We seem to experience time flowing, but if there are then an infinite number of instants then why don't we have an infinite number of experiences? Thus we have to think of a minimum interval of psychological time. Likewise in physics there is the Planck time (1.35×10-43 seconds) which might be thought of as a minimum interval of time. However this might not be the end - maybe there are shorter timescales. Think of weather forecasting. Computers have the values of quantities on a grid of points, but these are an approximation to the continuous nature of the atmosphere. However this is actually an approximation of the behaviour of individual atoms. These in turn are an approximation of continuous quantum wave functions. To model these on a computer we need to take a grid of points again. In the end whether we think of matter, space or time as being continuous or atomic is a metaphysical matter which has no bearing on what actually happens.

To some degree Lynds recognises this. He is careful to point out that his ideas aren't linked to the ideas of quantum uncertainty. However, he seems to think that his ideas supersede ideas which address the physical nature of time. Since his ideas are purely metaphysical, this cannot be the case. Interestingly all of the references within Lynds' paper are of this nature – referring to a fairly well known idea and saying that he supersedes it. There are no references to ideas which he is building upon. This is what really demonstrates the flaws in Lynds' work - he does not seem to have studied enough of the subjects which he is writing about to be able to make any meaningful advances.

It is interesting to look at some of the response to Lynds' paper. Some people seem to be arguing about whether he is right or wrong. This seems to be a sterile argument - I would say that he is right but not saying anything new. There seems to be a large body of opinion that Zeno's paradoxes are solved by Einstein's Special theory of relativity. Lynds disagrees with this, and I think I do too - it does not seem valid to deal with a paradox of classical theory by introducing 'new physics'. The fact that there real numbers are uncountable but the rationals are countable is sometimes brought up. I think this is a red herring - Zeno's paradoxes work entirely in the rationals (One solution to Zeno's paradox used non-standard numbers, which I found totally unconvincing). Lynds' work has been compared with that of Julian Barbour - people say that they have similar ideas. I disagree with this: Barbour says that only instants are important, while Lynds says that instants don't have any significance.

So Peter Lynds is much too arrogant, but then we all think that we're the new Einstein don't we? The news items about him seem to imply support from several well known physicists. However, on a closer look Wheeler's comments look like fairly standard replies to work sent to him, and Khrennikov has denied that his comments were supposed to support Lynds' ideas. It is a shame that no one said to Lynds 'well that's looks interesting, now why don't you learn something about the subject?' If he can learn a little humility and a lot of mathematics and physics then he may produce something worthwhile.
More References
A. N. Whitehead had similar ideas to Lynds: The Concept of Nature: Chapter 3: Time
An Epistemological Use of Nonstandard Analysis to Answer Zeno's Objections against Motion McLaughlin, W. I., and Miller, S. L. Synthese, 92: 371-384
Resolving Zeno's Paradoxes
McLaughlin, W. I. 		Scientific American, November 1994: 84-89

I feel that it is Foundations of Physics Letters which comes out badly from this affair. One wonders who at the journal actually read the paper. Not only did they fail to notice that this was essentially a metaphysical paper posing as physics, but Lynds makes a 'schoolboy error' in his paper of writing 2.7×10-21 (or maybe 2.7×10-22) as 2.7-21 . It's something which is easy to do but also easy to spot - but it is still in the printed version. Also it looks like an error has been introduced in the printed version which wasn't in the original:- η occurs in several well known equations in place of 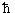. If journals cannot do better than this then I wonder what future there is for them in the internet dominated world.